Brain Waves
I was invited to work with Brad Voytek’s lab in the Cognitive Science department during the summer of 2020. Voytek Lab consists of 16 lab members ranging from undergraduate researchers to postdocs. Their interests are varied, but they primarily study neural oscillations from a computational neuroscience and experimental approach. In particular, they’re interested in how to quantify various statistics about neural oscillations and discerning whether certain statistics correlate with physiological traits.
Brad contacted me to see if I could help with a few things with their python package NeuroDSP. Beyond doing a basic technical audit for their digital signal processing toolkit, other ideas that were tossed around were looking at phase spectra of neuro signals, burst detection (eerily reminiscent of the indoor localization project), and fleshing out their simulations for unit testing and other methods comparisons. I ended up spending most of my time on the latter, partly because I quickly realized that neuro signals exhibit incredibly complex structure.
What You Can and Can’t Learn from the Periodogram
Any course in graduate time series analysis will spend lots of time analyzing ARMA models and stationary time series. In my case, the argument for reducing from nonstationary to stationary time series didn’t even take a whole lecture and effectively amounted to centering the time series, and then looking at the periodogram and subtracting off cosines until the spectrum lacks any obvious peaks. If you want to get fancy, you could fit local linear models for trend estimation instead of assuming a constant trend.
Forget for a moment that any interesting time series is interesting precisely because of its nonstationarities. This by now classical signal processing approach of looking at the periodogram for indications of oscillatory behavior is not without its strengths but certainly falls short in many contexts. Its strength of course is all of the theory that comes with the Fourier transform. All periodic signals can be decomposed as sums of sines and cosines, and trigonometric oscillations like sine and cosine are easy to spot as spikes in the periodogram. Issues start arising when you start having sharp, near discontinuous oscillations like a square wave or a sawtooth wave. Looking only at the periodogram, you’ll find peaks at harmonics of the fundamental frequency of these waves, a broadband effect of but a single oscillating signal. The problem in practice though is you don’t get to see the full spectrum. The frequency range you observe is limited by your sampling rate, so as an inverse problem you’re left to wonder: given this periodogram with spikes at harmonic frequencies, am I looking at a finite sum of cosines, or something else?
The more glaring issue is that the periodogram ignores half of the information provided by the Fourier transform, namely phase. Without it, you’ll have hard time telling the difference between an impulse–or a dirac spike–and pure white noise. That these two signals have radically different temporal structures yet qualitatively the same power spectrum should raise alarms about ignoring phase data. That phase is just as critical as amplitude is evidenced by the fact that phase retrieval is an area of active research to this day.
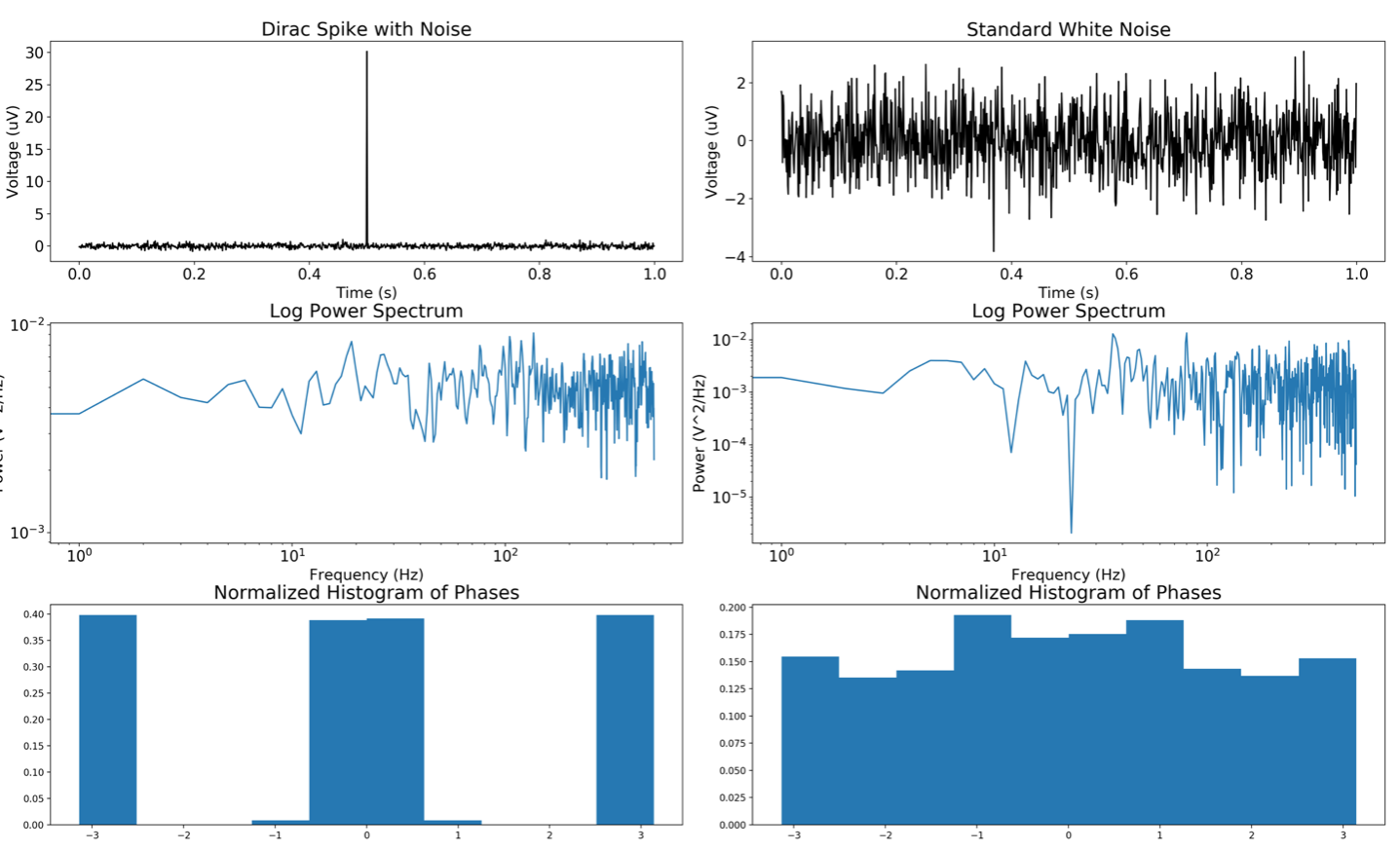 |
| Fig. 1: White noise and an impulse both have flat power spectra, yet their temporal structure and their phase distributions are quite different. |
What’s Your Favorite Anagram of Fractal Noise?
The examples I’ve raised so far are ultimately non-issues in the absence of noise. Even ignoring phase, if you looked at the time series data itself you could discern between sums of cosines and a square wave, an impulse and white noise. Noise obfuscates all of this, particularly neural noise. When I started working with Brad’s then Ph.D. student Tom Donoghue, we spent a lot of time talking about “the aperiodic component” of neuro signals. There is no precise definition of what the aperiodic component is, but empirical evidence suggests that measurements of brain activity from, say, EEG readings, tend to feature a signal component, believed to be noise, whose power spectrum obeys a simple power law \[|\hat{x}(\omega)|^2 \propto \frac{1}{\omega^{\chi}}\] or a multiple power law \[|\hat{x}(\omega)|^2 \propto \frac{1}{\omega^{\chi_1}(\omega^{\chi_2} + k)}.\]
Mother nature seems to have a knack for power laws, so I guess this shouldn’t be terribly surprising. They appear in various laws of physics, in hydrological data, atmospheric data, distribution of wealth and settlement sizes. As a statement about power spectra, there’s nothing immediately concerning about this statement. However, under the assumption that the aperiodic component is a random process, the complexity of neural noise begins to rear its head in the autocorrelation function. Provided the time series is stationary, the autocorrelation function is a univariate function of the lag and is related to the power spectrum via the Fourier transform. As it so happens, Fourier maps power laws to power laws, and autocorrelation functions that obey a power law are known as “long memory processes.” Curiously, long memory processes are intimately related to self-similar processes which exhibit fractal like behavior.
By the time I’ve realized this I’ve started to realize the gravity of the problem in detecting neural oscillations. Beyond dealing with time varying oscillations like bursts and potentially non-sinusoidal oscillations, you’re mixing these signals with a fractal noise process whose autocorrelation function may not even be absolutely summable or, worse, may not even exist due to nonstationarity. Both cases are alarming because the periodogram may not even be a consistent estimator of the power spectrum and discrete simulations of these kinds of processes introduce a host of subtle, but critical issues.
I’ll admit when I was building simulations for neural noise I was not fully aware of the kinds of complications and subtleties that arise based on discretization and what statistics you choose to match. For example, it’s fairly straightforward to construct a simulation of a fractional gaussian noise process whoses empirical autocorrelation function is close to the true autocorrelation function. It turns out, however, that this introduces bias in the empirical periodogram. Nearly all of the computational neuroscience literature I came across assumed without proof that time series whose periodogram exhibited a power law either fell into the fractional gaussian noise model or the fractional brownian motion model depending on the exponent of the power law, so I spent my time understanding these processes. I had a hard time finding a proof of such a claim in a mathematical context. I later found out that there is a litany of processes which also exhibit power spectra with power laws such as chaotic Hamiltonian systems, periodically driven bi-stable systems, running maxima of Brownian motion, ionic nanopore currents, to name a few. A lot of scientific research has been done on the brain, and yet we still know so little about the generating process of neural oscillations and neural noise. Without an informing prior, it’s hard to choose a generating process for simulations.
Is It All Just Central Limit Theorem?
Realizing how deep and cavernous this rabbit hole was, I decided to keep my simulations pretty simple. NeuroDSP now features simulations for fractional gaussian noise and fractional brownian motion. Beyond that, it also has simulations to construct signals with an arbitrary power spectrum shape by summing a bunch of weighted cosines with uniform random phase shifts. There’s nothing deep about this sum-of-sines approach, but its simplicity allows for precise parametrization of power spectra which is very useful for accuracy testing various computational neuroscience methods that claim to detect aperiodic signal statistics based off the periodogram. NeuroDSP had two other ways of simulating aperiodic noise using filtered white noise. At the end of the summer I decided to look at what the qualitative differences between these various simulations were in the Fourier domain. Much to my surprise, the differences were very hard to spot from amplitude, phase, and time series data alone.
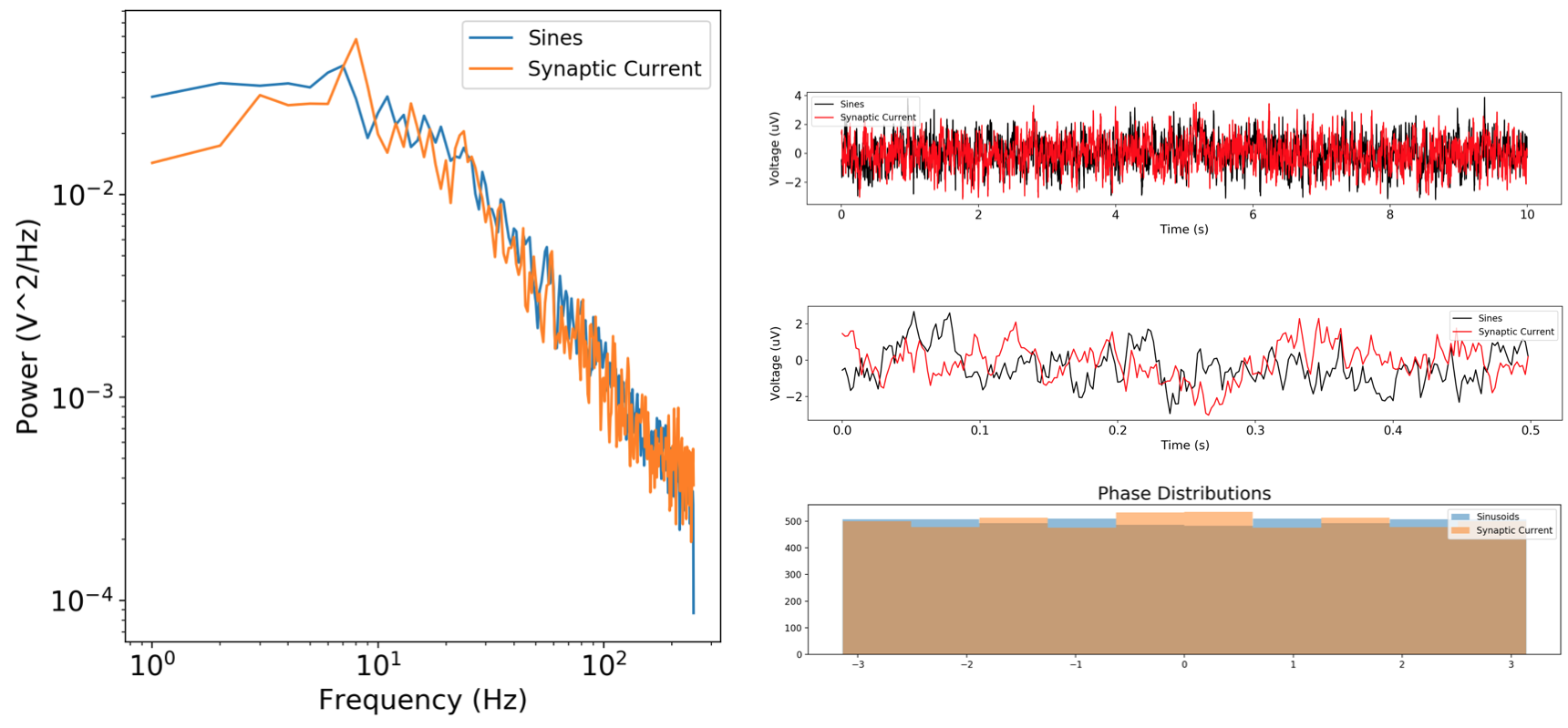 |
| Fig. 2: Sum of sinusoids signal plotted against a simulation of a synaptic current. Both feature multiple power law structure in the periodogram, also known as multifractal behavior. |
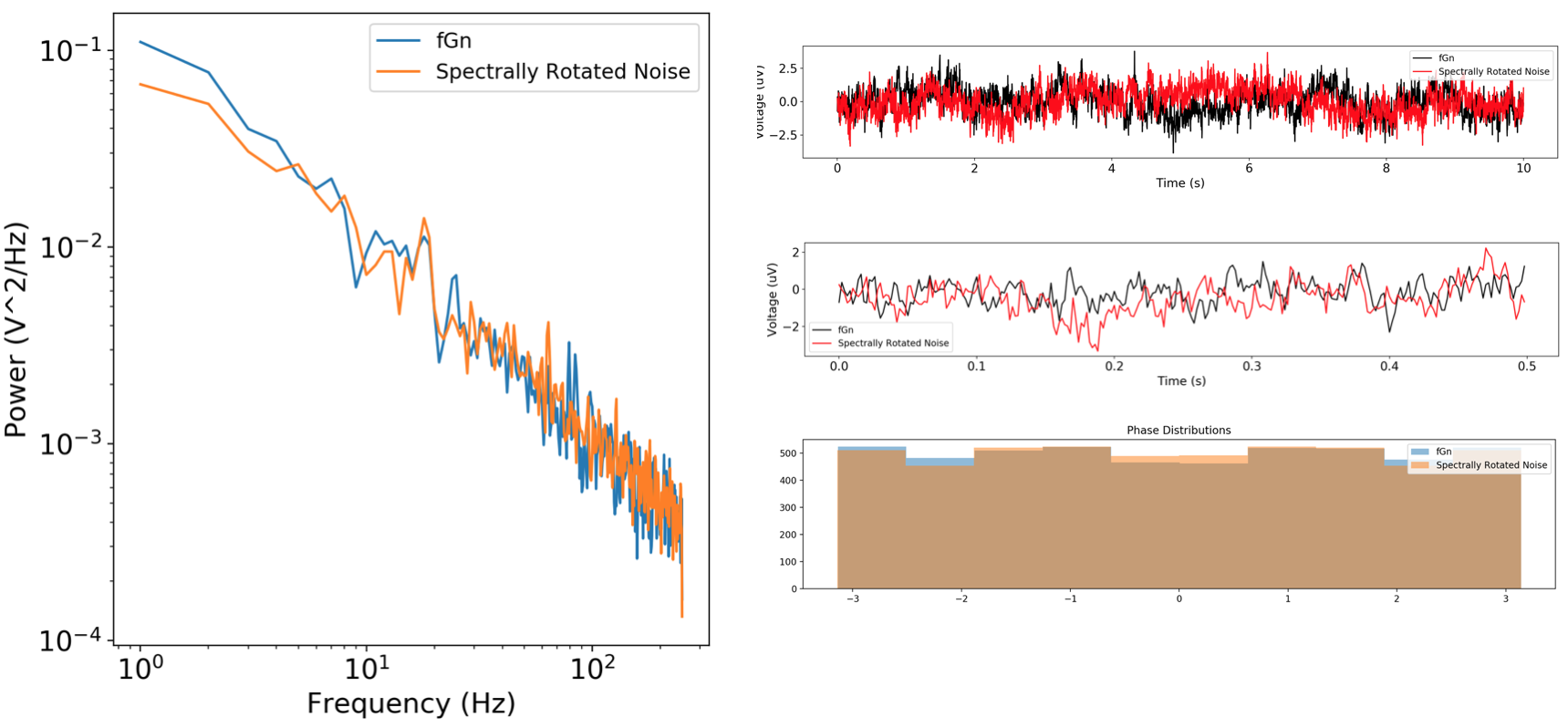 |
| Fig. 3: Fractional gaussian noise plotted against spectrally rotated noise. The latter is generated by applying a rotation to white noise in the Fourier domain, taking the inverse Fourier transform, and taking the real part of that complex-valued time series. |
Part of this was by construction I guess. The fact that all of the phase distributions came out uniform was a bit of a surprise, at least in the fractional noise settings. I couldn’t find any resources that gave analytic distributions for the phase of fractional gaussian noise or fractional brownian motion, but I didn’t look too deeply since I was trying to stay away from rabbit holes with the limited time I had. I can see it for fractional gaussian noise since having an absolutely summable autocorrelation function ensures that the coordinates in the Fourier series are approximately independent complex gaussians because of central limit theorem. Of course, it could be the case that in the setting where the autocorrelation function is not absolutely summable that a generalized central limit theorem is kicking in and the limiting distribution is some Levy stable distribution that is not gaussian.
By the time my contract with Voytek Lab has ended, I’m left with more questions about long memory processes than I came in with. The implications of understanding these kinds of stochastic processes better is more than just a mathematical breakthrough as is now clear to me. That’s a big reason why I like working with other scientists. Beyond the excitement of collaborating with other people, it’s easy to slip into the misleading mentality that most of the practical issues of math have been sorted out and the rest is just engineering. After all, humanity has had a long time to think about math ever since the Babylonians stumbled upon arithmetic. This is particularly true if you spend most of your time thinking about proving theorems about other people’s problems like phase retrieval, blind deconvolution, and deep learning all while staying behind the closed doors of the math department. Standing in stark contrast to this is the wild west of fields like Cognitive Science which are quite young in comparison, incredibly interdisciplenary, and asking fundamental questions about how our brains work. If anything, the fact that cognitive science is grappling with complex problems like fractal time series should be a call for more collaboration between mathematicians and other fields of science.
