Robots & Calculus

In 2017, I built a robot arm from the InMoov project for my multivariable calculus students. This class starts with vectors and ends with differential forms, manifolds, and Stokes’ theorem. I was inspired by my fatigue of qualifying exam courses and the lineage of mathematicians at UGA who also built robot arms (shout out to David Millard and Jason Cantarella).

Robotics turns out to be a surpsingly good motivation for a lot of topics in multivariable calculus. I had originally set out to use the robot arm as a motivator for manifolds since I had a hard time wrapping my head around what a manifold was when I first learned about them. The classic quote by topologist Schmuel Weinberger succintly describes what most math students come to realize in their first course on manifolds: “manifolds are a bit like pornography: hard to define, but you know one when you see one.” There are plenty of contexts where manifolds naturally appear such as differential geometry and mathematical physics. Having taught math for now 5+ years though I can tell you that very few first and second year math students daydream about differential geometry or mathematical physics. On the other hand, I have found that students do get excited about modern and tangible applications of math.

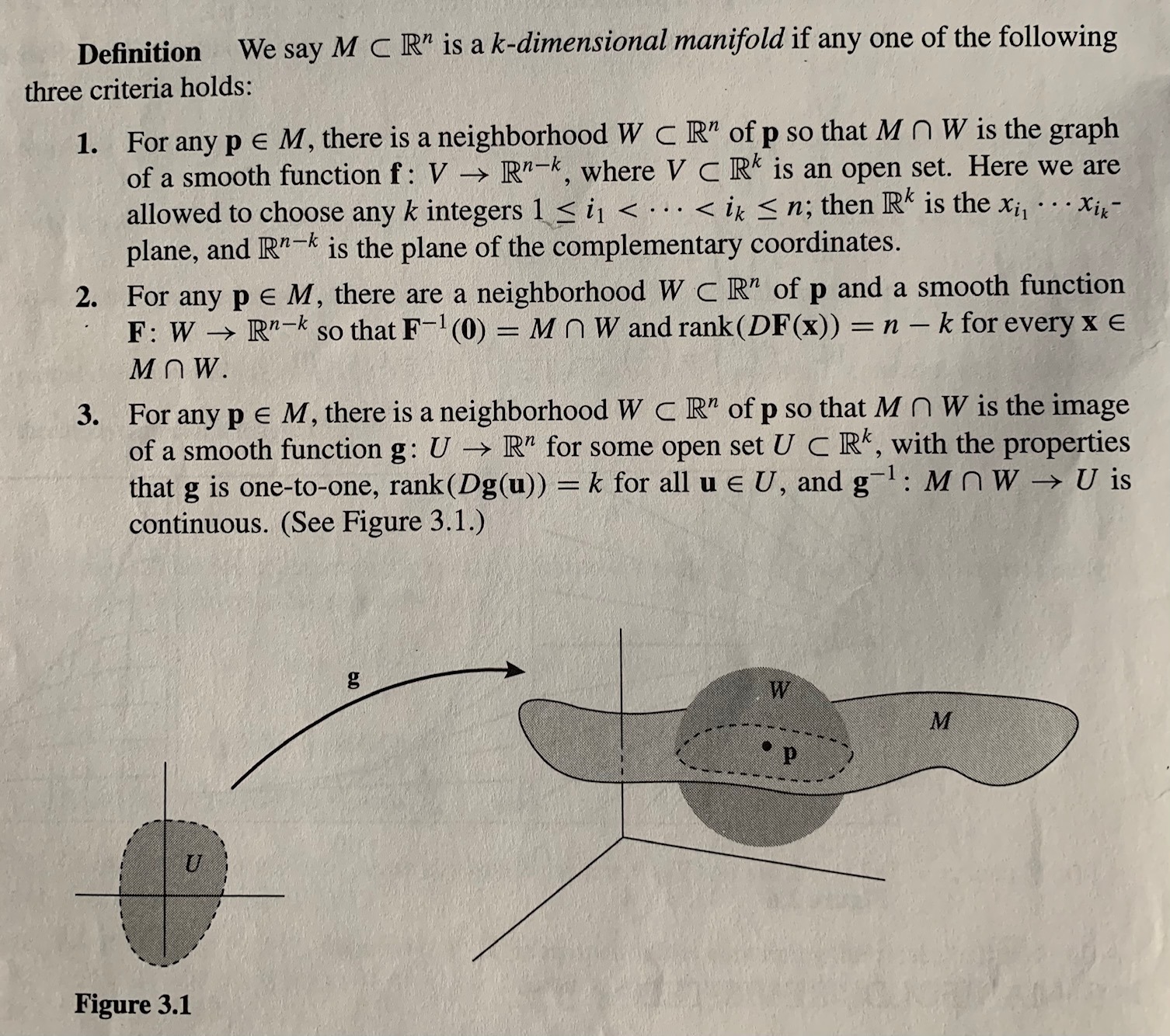Fig. 1: The formal definition(s) of a manifold.

What I Learned From Building

I’ll admit I went into this project blindly. I started in January thinking I would have plenty of time to 3D print the pieces, assemble them, and have a demo ready by March. This ended up being an overly optimistic timeline. My responsibilities as a student and a teaching assistant aside, the logistics of 3D printing the pieces were more complicated than I first thought. All my 3D printing happened at UCSD’s Digital Media Lab. This is an incredible service provided through the campus library and it allowed me to print all of my parts at no cost. However, I was competing with lots of engineering students for access to these printers. Furthermore, I could only reserve a printer for 3 hours a day. Anyone who has done any 3D printing can tell you that 3 hours is not that much time to print even modestly sized objects, and some prints can be very error prone. The print could fail to adhere to the build plate. The heating element in the extruder could drop a few degrees and the filiment could clog the extruder. The build plate could be uneven. The extruder could be miscalibrated, or slip. A clumsy passerby could accidentally hit your print. Some prints are awkward for a 3D printer parameterized with Cartesian coordinates (think spheres and thin, curved sheets). Any of these errors could cause issues at any time, especially near the end of a very long print.

The logistics notwithstanding, I ended up learning a lot about 3D printers because I wasn’t guaranteed a dedicated printer. The models that the Digital Media Lab had at the time included a few Makerbot Replicators, an Ultimaker 2+, a Prusa i3 MK2, and a HE3D K280. For the record, when I eventually purchase a 3D printer the Prusa will be near if not at the top of my list. Not only is it the cheapest option among the ones I listed, it also gave some of the highest quality prints for my robot arm. The Ultimaker 2+ came pretty close but the price tag was 3x that of the Prusa. Apparently I’m not alone in thinking that the Prusa is superior. As of the time of this writing the Digital Media Lab has replaced all of their 3D printers with Prusas.

Naturally there were issues even once I had all of the parts printed. Hours were spent carefully sanding pieces so that they fit together just right (“beware the build up of frictional forces” my Digital Media Lab Sensei Miguel de Villa often reminded me). The fishing line that the servomotors pulled to contract the fingers might snap or come undone. Even though I hadn’t anticipated any of these issues, a part of me enjoyed these small challenges. These kinds of issues are entirely different than the problems that were occupying my time in my numerical analysis qual class. These hardware issues reminded me to appreciate good engineering.

Fig. 2: A near complete robot arm.

What (I Hope) My Students Took Away

By the time the calculus class got to manifolds I had finished printing the right arm for the InMoov robot and had the left arm half assembled. The right arm was sufficient to talk to my students about a lot of concepts they learned over the year long sequence. We spent time talking about how manifolds model configuration spaces for robots, how vector fields and a little bit of electricity and magnetism explain how the servomotors powering the arm operate. We even got to talk a bit about my woes with Cartesian coodinates when 3D printing quadrants of the forearm which are naturally more cylindrical than cubical.

My students really got a kick out of the robot arm. Unlike the analogous course I took at UGA, this batch of multivariable calculus students had a pretty diverse set of majors which included math, physics, pre-med, biology, and engineering majors. I never worried about motivating the course for the physics students since physics is comfortably couched in many calculus problems. I did worry about motivating calculus for those students who weren’t pursuing degrees in the physical sciences, or maybe hadn’t yet decided what they wanted to study. I remember being pretty clueluess about what I wanted to do up until halfway through undergrad. The only reason I had enrolled in math classes were to satisfy prerequisites for my then physics major classes. It wasn’t until I took numerical analysis at UGA did I understand just how broadly applicable subjects like calculus and linear algebra were. That class was truly magical, in no small part due to how well Jason Canterella designed it. It was project based, and the students competed against one another. Our optimization project had us code up various non-convex optimization algorithms to find the shortest path across an actual mountain range parameterized by topographic coordinates. Our differential equations project was to solve for the initial firing velocity and the angle at which to fire a rail gun from Pearl Harbor to hit a boat many miles west in the Pacific. We ended our numerical linear algebra studies by designing an image compression algorithm (my friend Fred won that one). Learning finite element method, Nelder-Mead, and the singular value decomposition was one thing. Using those tools to solve legitimately interesting problems stirred my spirit.

So I guess I was trying to recreate that sense of wonder that I had in my undergrad for my students. Like great teaching, that sense of wonder is hard to quantify. If I happened to inspire, however briefly, anyone in that quarter of MATH 31CH then I’ll consider my mission accomplished.